TEXTOVÝ PREPIS LEKCIE:
Myšlienka roviny v priestore nám umožňuje získať napríklad povrch stola alebo steny. Stôl alebo stena má však konečné rozmery a rovina siaha za jej hranice do nekonečna.
Zvážte dve pretínajúce sa roviny. Keď sa pretínajú, zvierajú štyri uhly dvojsteny so spoločnou hranou.
Pripomeňme si, čo je dihedrálny uhol.
V skutočnosti sa stretávame s predmetmi, ktoré majú tvar uholníka: napríklad mierne otvorené dvierka alebo pootvorený priečinok.
Keď sa pretínajú dve roviny alfa a beta, získame štyri dihedrálne uhly. Nech sa jeden z uhlov klinu rovná (phi), potom sa druhý rovná (1800 -), tretí, štvrtý (1800 -).
Zvážte prípad, keď je jeden z uhlov klinu 900.
Potom sa v tomto prípade všetky dihedrálne uhly rovnajú 900.
Uveďme definíciu kolmých rovín:
Dve roviny sa nazývajú kolmé, ak je uhol medzi nimi 90°.
Uhol medzi rovinami sigma a epsilon je 90 stupňov, čo znamená, že roviny sú kolmé
Uveďme príklady kolmých rovín.
Stena a strop.

Bočná stena a stolová doska.
Formulujme znamienko kolmosti dvoch rovín:
TEÓZA: Ak jedna z dvoch rovín prechádza priamkou kolmou na druhú rovinu, potom sú tieto roviny kolmé.
Dokážme toto znamenie.
Podľa podmienky je známe, že priamka AM leží v rovine α, priamka AM je kolmá na rovinu β,
Dokážte: roviny α a β sú kolmé.
dôkaz:
1) Roviny α a β sa pretínajú pozdĺž priamky AR, zatiaľ čo AM je AR, pretože AM je podľa podmienky β, to znamená, že AM je kolmá na akúkoľvek priamku ležiacu v rovine β.
2) Nakreslíme priamku AT kolmú na AP v rovine β.
Dostaneme uhol TAM - lineárny uhol dihedrálneho uhla. Ale uhol TAM = 90°, keďže MA je β. Takže α β.

Q.E.D.
Zo znamienka kolmosti dvoch rovín máme dôležitý dôsledok:
DÔSLEDOK: Rovina kolmá na priamku, pozdĺž ktorej sa pretínajú dve roviny, je kolmá na každú z týchto rovín.
To znamená: ak α∩β=с a γ с, potom γ α a γ β.
Dokážme tento dôsledok: ak je rovina gama kolmá na priamku c, potom na základe rovnobežnosti dvoch rovín je gama kolmá na alfa. Rovnako gama je kolmá na beta
Preformulujme tento dôsledok pre dihedrálny uhol:
Rovina prechádzajúca lineárnym uhlom dihedrálneho uhla je kolmá na hranu a strany tohto dihedrálneho uhla. Inými slovami, ak sme skonštruovali lineárny uhol dihedrálneho uhla, potom rovina prechádzajúca ním je kolmá na hranu a steny tohto dihedrálneho uhla.
Dané: ΔABC, C = 90°, AC leží v rovine α, uhol medzi rovinami α a ABC = 60°, AC = 5 cm, AB = 13 cm.
Nájdite: vzdialenosť od bodu B k rovine α.

1) Zostrojme VC α. Potom KS je projekcia slnka na túto rovinu.
2) BC AC (podľa podmienky), čo znamená podľa vety o troch kolmých (TPP) KS AC. Preto VSK je lineárny uhol dihedrálneho uhla medzi rovinou α a rovinou trojuholníka ABC. To znamená, že VSK = 60°.
3) Z ΔBCA podľa Pytagorovej vety:
Odpoveď VK sa rovná 6 koreňom po troch cm
Praktické využitie (aplikovaný charakter) kolmosti dvoch rovín.
Konštrukcia dvoch vzájomne kolmých rovín. Ako je známe, roviny sú kolmé, ak priamka patriaca do jednej roviny je kolmá na inú rovinu. Preto môže byť rovina kolmá na danú rovinu vedená cez priamku kolmú na danú rovinu alebo kolmú na priamku ležiacu v danej rovine.
Na obr. Roviny 4.12 (rovina trojuholníka ABC a rovina P) sú navzájom kolmé, keďže rovina P je kolmá na priamku A1 ležiacu v rovine trojuholníka. Priemet roviny P prechádzajúcej priamkou s priemetmi m 2 n 2, m 1 n 1 a kolmou na rovinu určenú priemetmi a 2 b 2 c 2, a 1 b 1 c 1 trojuholníka je znázornený na obr. Obr. 4.12.
Konštrukcia: 1. Nakreslite hlavné čiary roviny, C1 - horizontálne, C2 - čelné.
2. Cez ľubovoľný bod E (umiestnený mimo trojuholníka ABC) nakreslite priamku EF kolmú na hlavné čiary roviny (c 2 f 2 je kolmá na c 2 2 2 a c 1 f 1 je kolmá na 1 1 1).
3. Cez bod N nakreslite ľubovoľnú priamku EM pretínajúcu sa s EF, získame rovinu P definovanú dvoma pretínajúcimi sa priamkami (EM X EF).
Rovina P(ME X EF) je teda kolmá na rovinu Q(trojuholník ABC).
Treba poznamenať, že pre vzájomne kolmé roviny všeobecné postavenie ich rovnomenné stopy nie sú nikdy kolmé. Ale ak jedna z daných rovín (alebo obe) je všeobecná rovina, potom vzájomná kolmosť na diagrame jednej dvojice ich stôp udáva kolmosť rovín v priestore.
18) Priamku priesečníka dvoch rovín možno určiť ich dvoma spoločnými bodmi. Na tento účel určte priesečníky akýchkoľvek dvoch priamok jednej roviny s inou rovinou alebo priesečníky priamky na každej z rovín s inou rovinou.
Konštrukčná postupnosť:
Priesečník dvoch rovín možno nájsť pomocou pomocných rezných rovín pri riešení. Zvyčajne sa vyberajú projekčné roviny (často horizontálne alebo čelné)
Vyberte ľubovoľnú sečnicu pomocnú horizontálnu rovinu Ф1, ktorá pretína dané roviny pozdĺž priamok (12 a 34), ktoré sa (na p1 pretínajú v bode k)
Druhá sečná horizontálna rovina pretína dané roviny aj pozdĺž horizontál, tie sa zasa pretínajú v bode E
Priama KE je priesečník daných rovín.
Uvažujme o riešení tohto problému na plochom výkrese.
1. etapa riešenia Na zostrojenie bodu M sa používa vodorovne premietajúca rovina - prostredník ("), ktorý uzatvára stranu AB trojuholníka ABC.
2. etapa riešenia Zostrojíme priesečník (na výkrese je určený bodmi 1 a 2) medziroviny (“) a roviny DEK.
3. fáza riešenia Nájdite bod M priesečníka priamky 1 - 2 s priamkou AB.
Bol nájdený jeden bod M požadovanej priesečníkovej čiary.
Na zostrojenie bodu N sa používa vodorovne premietaná rovina (“), ktorá obklopuje stranu AC trojuholníka ABC.
Konštrukcie sú podobné predchádzajúcim.
Určenie viditeľnosti v rovine H sa vykonáva pomocou horizontálne konkurujúcich bodov 4 a 8
Bod 4 sa nachádza nad bodom 8 (4" a 8"), takže na rovine H časť trojuholníka DEK, ktorá sa nachádza smerom k bodu 4, prekrýva časť trojuholníka ABC, ktorá sa nachádza od priesečníka smerom k bodu 8. Pomocou určí sa dvojica čelne konkurujúcich bodov 6 a 7 viditeľnosť na rovine V.

Priesečník dvoch čelne vyčnievajúcich rovín (?)
Priesečník dvoch vodorovne vyčnievajúcich rovín (?)
19) Rez je obraz predmetu mentálne rozrezaný jednou alebo viacerými rovinami, pričom mentálna disekcia predmetu sa týka iba tohto rezu a nespôsobuje zmenu v iných obrazoch toho istého predmetu. Sekcia ukazuje čo sa nachádza v rovine rezu a čo sa nachádza za ňou.
V závislosti od počtu sečných rovín je sekcia rozdelená na:
Jednoduché (s jednou rovinou rezu)
Komplexné (s niekoľkými rovinami rezu)
V závislosti od polohy roviny rezu vzhľadom na vodorovnú projekčnú rovinu sú rezy rozdelené na:
HORIZONTÁLNA – rovina rezu je rovnobežná s horizontálnou premietacou rovinou
VERTIKÁLNE - rovina rezu je kolmá na horizontálnu projekčnú rovinu
ŠIKMÁ - rovina rezu je nejaký nepriamy uhol s vodorovnou rovinou =) ZVISLÝ rez je tzv čelný ak je rovina rezu rovnobežná s čelnou rovinou výstupkov. A profilu ak je rovina rezu rovnobežná s profilovou rovinou výstupkov.
KOMPLEXNÉ rezy sú POZDĹŽNE, ak sú rezné roviny nasmerované po dĺžke alebo výške predmetu. A PRÍČNE, AK sú roviny rezu nasmerované KOLMO na dĺžku alebo výšku predmetu.
KROK – ak sú sečné roviny navzájom rovnobežné
BROKEN – ak sa roviny rezu navzájom pretínajú.
LOCAL rezy slúžia na odhalenie vnútornej štruktúry objektu na samostatnom ohraničenom mieste. LOCAL SECTION je v pohľade zvýraznený pevnou, vlnitou, tenkou čiarou.
Označenie rezov - Poloha roviny rezu je označená otvorenou čiarou rezu. Začiatočný a koncový ťah čiary rezu by nemal pretínať obrys príslušného obrázku. Šípky by mali byť umiestnené na počiatočný a konečný ťah označujúci smer pohľadu.Šípky by mali byť umiestnené vo vzdialenosti 2...3 mm od vonkajšieho konca ťahu.
PRE KOMPLEXNÝ REZ sa ťahy otvorenej čiary rezu kreslia aj na ohyboch čiary rezu.
V BLÍZKOSTI šípok označujúcich smer pohľadu sú na vonkajšej strane rohu použité veľké písmená ruskej abecedy. Označenia písmen sú priradené v abecednom poradí bez opakovania alebo vynechania.
Samotný rez by mal byť označený nápisom ako A-A
Ak sa sečná rovina zhoduje s rovinou symetrie objektu a rez je vytvorený na mieste zodpovedajúceho pohľadu v projekčnom spojení, potom pre horizontálne, čelné a profilové rezy nie je potrebné označovať polohu sečnej roviny. a strih nie je doplnený nápisom.
Ak sa obrysová čiara objektu zhoduje s osou symetrie, potom je hranica medzi pohľadom a rezom označená vlnovkou, ktorá je nakreslená tak, aby sa zachoval obraz hrany.
Dve roviny, ktoré sa pretínajú, sa nazývajú kolmý, ak tretia rovina, kolmá na priesečník týchto dvoch rovín, ich pretína pozdĺž kolmých čiar (pozri obrázok).Akákoľvek rovina kolmá na priesečník kolmých rovín ich pretína pozdĺž kolmých čiar.
Znak kolmosti rovín
Veta 1. Ak rovina prechádza priamkou kolmou na inú rovinu, potom sú tieto roviny kolmé (pozri obrázok). 
Veta 2. Ak je priamka ležiaca v jednej z dvoch kolmých rovín kolmá na priamku ich priesečníka, potom je kolmá aj na druhú rovinu (pozri obrázok).
Príklad aplikácie vety 2
Nech existujú dve kolmé roviny, ktoré sa pretínajú v priamke a(pozri obrázok). Nájdite vzdialenosť od bodu A, ktorá leží v rovine a neleží v rovine, rovine.
V rovine zostrojíme kolmicu k a cez bod A. Nechajte ho prejsť a v bode B. AB- požadovaná vzdialenosť.
Venujte pozornosť tomuto.
1. Cez bod mimo roviny možno nakresliť veľa rovín kolmých na túto rovinu (pozri obrázok). (Všetky však prejdú priamkou kolmou na túto rovinu, ktorá prechádza daným bodom.)

2. Ak je rovina kolmá na danú rovinu, neznamená to, že je kolmá na ľubovoľnú priamku rovnobežnú s touto rovinou.
Napríklad na obrázku nižšie a pretínajú sa v priamke b, a a vchádza do jednej z rovín a . Preto rovno a súčasne rovnobežné s dvoma na seba kolmými rovinami.

Pojem kolmých rovín
Keď sa pretínajú dve roviny, dostaneme uhly 4$. Dva uhly sa rovnajú $\varphi $ a ďalšie dva sa rovnajú $(180)^0-\varphi $.
Definícia 1
Uhol medzi rovinami je minimom dihedrálnych uhlov tvorených týmito rovinami.
Definícia 2
Dve pretínajúce sa roviny sa nazývajú kolmé, ak uhol medzi týmito rovinami je $90^\circ$ (obr. 1).
Obrázok 1. Kolmé roviny
Znak kolmosti dvoch rovín
Veta 1
Ak je priamka roviny kolmá na inú rovinu, potom sú tieto roviny navzájom kolmé.
Dôkaz.
Dajme nám roviny $\alpha $ a $\beta $, ktoré sa pretínajú pozdĺž priamky $AC$. Priamka $AB$ ležiaca v rovine $\alpha $ nech je kolmá na rovinu $\beta $ (obr. 2).
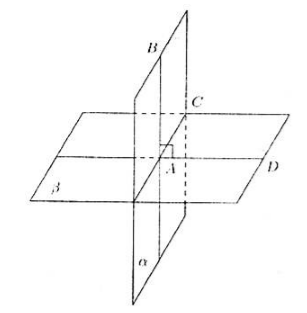
Obrázok 2
Keďže priamka $AB$ je kolmá na rovinu $\beta$, je kolmá aj na priamku $AC$. Dodatočne nakreslíme priamku $AD$ v rovine $\beta$, kolmú na priamku $AC$.
Zistili sme, že uhol $BAD$ je lineárny uhol dihedrálneho uhla, rovný $90^\circ$. To znamená, že podľa definície 1 je uhol medzi rovinami $90^\circ$, čo znamená, že tieto roviny sú kolmé.
Veta bola dokázaná.
Z tejto vety vyplýva nasledujúca veta.
Veta 2
Ak je rovina kolmá na priamku, pozdĺž ktorej sa pretínajú dve ďalšie roviny, potom je tiež kolmá na tieto roviny.
Dôkaz.
Dajme nám dve roviny $\alpha $ a $\beta $ pretínajúce sa pozdĺž priamky $c$. Rovina $\gama $ je kolmá na priamku $c$ (obr. 3)

Obrázok 3.
Keďže priamka $c$ patrí rovine $\alpha $ a rovina $\gamma $ je kolmá na priamku $c$, potom podľa vety 1 sú roviny $\alpha $ a $\gamma $ kolmé.
Keďže priamka $c$ patrí rovine $\beta $ a rovina $\gamma $ je kolmá na priamku $c$, potom podľa vety 1 sú roviny $\beta $ a $\gamma $ kolmé.
Veta bola dokázaná.
Pre každú z týchto teorém platia aj opačné tvrdenia.
Vzorové problémy
Príklad 1
Dajme nám pravouhlý rovnobežnosten $ABCDA_1B_1C_1D_1$. Nájdite všetky dvojice kolmých rovín (obr. 5).

Obrázok 4.
Riešenie.
Podľa definície pravouhlého rovnobežnostena a kolmých rovín vidíme nasledujúcich osem párov rovín navzájom kolmých: $(ABB_1)$ a $(ADD_1)$, $(ABB_1)$ a $(A_1B_1C_1)$, $( ABB_1)$ a $(BCC_1) $, $(ABB_1)$ a $(ABC)$, $(DCC_1)$ a $(ADD_1)$, $(DCC_1)$ a $(A_1B_1C_1)$, $(DCC_1) $ a $(BCC_1)$, $(DCC_1)$ a $(ABC)$.
Príklad 2
Dajme nám dve navzájom kolmé roviny. Z bodu v jednej rovine je nakreslená kolmica na inú rovinu. Dokážte, že táto priamka leží v danej rovine.
Dôkaz.
Dajme nám kolmé roviny $\alpha $ a $\beta $ pretínajúce sa pozdĺž priamky $c$. Z bodu $A$ roviny $\beta $ je na rovinu $\alpha $ nakreslená kolmica $AC$. Predpokladajme, že $AC$ neleží v rovine $\beta$ (obr. 6).
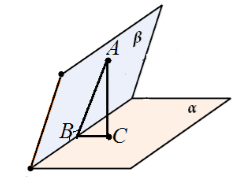
Obrázok 5.
Zvážte trojuholník $ABC$. Je obdĺžnikový s pravým uhlom $ACB$. Preto $\uhol ABC\ne (90)^0$.
Ale na druhej strane $\uhol ABC$ je lineárny uhol dihedrálneho uhla, ktorý tvoria tieto roviny. To znamená, že dihedrálny uhol tvorený týmito rovinami sa nerovná 90 stupňom. Zistili sme, že uhol medzi rovinami sa nerovná $90^\circ$. Rozpor. Preto $AC$ leží v rovine $\beta$.
Kolmosť v priestore môže mať:
1. Dve rovné čiary
3. Dve roviny
Pozrime sa postupne na tieto tri prípady: všetky definície a výroky teorémov, ktoré s nimi súvisia. A potom budeme diskutovať o veľmi dôležitej vete o troch kolmiciach.
Kolmosť dvoch čiar.
Definícia:
Dá sa povedať: aj pre mňa objavili Ameriku! Pamätajte však, že vo vesmíre nie je všetko také isté ako v lietadle.
Na rovine môžu byť kolmé iba nasledujúce čiary (pretínajúce sa):
Ale dve priame čiary môžu byť kolmé v priestore, aj keď sa nepretínajú. Pozri:

priamka je kolmá na priamku, hoci sa s ňou nepretína. Ako to? Pripomeňme si definíciu uhla medzi priamkami: ak chcete nájsť uhol medzi pretínajúcimi sa čiarami a, musíte nakresliť priamku cez ľubovoľný bod na priamke a. A potom sa uhol medzi a (podľa definície!) bude rovnať uhlu medzi a.
Pamätáš si? No, v našom prípade, ak sa priame čiary a ukážu ako kolmé, potom musíme zvážiť priame čiary a byť kolmé.
Pre úplnú prehľadnosť sa pozrime na príklad. Nech je tam kocka. A budete požiadaní, aby ste našli uhol medzi čiarami a. Tieto čiary sa nepretínajú – pretínajú sa. Ak chcete nájsť uhol medzi a, nakreslite.

Vzhľadom na to, že ide o rovnobežník (a dokonca aj obdĺžnik!), ukazuje sa, že. A vzhľadom na to, že ide o štvorec, ukazuje sa, že. No to znamená.
Kolmosť priamky a roviny.
Definícia:
Tu je obrázok:

priamka je kolmá na rovinu, ak je kolmá na všetky, všetky priamky v tejto rovine: a, a, a, a dokonca! A miliarda ďalších priamych!
Áno, ale ako potom môžete všeobecne skontrolovať kolmosť v priamke a v rovine? Takže život nestačí! Ale našťastie pre nás, matematici nás zachránili pred nočnou morou nekonečna tým, že vymysleli znak kolmosti priamky a roviny.
Poďme formulovať:
Ohodnoťte, aké je to skvelé:

ak sú v rovine, na ktorú je priamka kolmá, iba dve priame čiary (a), potom sa táto priamka okamžite ukáže ako kolmá na rovinu, to znamená na všetky priame čiary v tejto rovine (vrátane niektorých priamych čiara stojaca na boku). Toto je veľmi dôležitá veta, preto jej význam nakreslíme aj vo forme diagramu.

A pozrime sa znova príklad.
Daj nám pravidelný štvorsten.

Úloha: dokázať to. Poviete si: to sú dve rovné čiary! Čo s tým má spoločné kolmosť priamky a roviny?!
Ale pozri:

označíme stred okraja a nakreslíme a. Toto sú mediány v a. Trojuholníky sú pravidelné a...
Tu je zázrak: ukazuje sa, že od a. A ďalej na všetky priame čiary v rovine, čo znamená a. Dokázali to. A najdôležitejším bodom bolo práve použitie znamienka kolmosti priamky a roviny.
Keď sú roviny kolmé
Definícia:

To znamená (ďalšie podrobnosti nájdete v téme „uhol klinu“) dve roviny (a) sú kolmé, ak sa ukáže, že uhol medzi dvoma kolmicami (a) k priesečníku týchto rovín je rovnaký. A existuje veta, ktorá spája pojem kolmých rovín s pojmom kolmosť v priestore priamky a roviny.
Táto veta sa nazýva
Kritérium kolmosti rovín.
Poďme formulovať:
Ako vždy, dekódovanie slov „vtedy a až potom“ vyzerá takto:
- Ak, tak prechádza cez kolmicu na.
- Ak prechádza cez kolmicu k, potom.
(samozrejme, tu sme lietadlá).
Táto veta je jednou z najdôležitejších v stereometrii, ale, žiaľ, aj jednou z najťažšie aplikovateľných.
Takže musíte byť veľmi opatrní!
Takže znenie:

A opäť dešifrovanie slov „vtedy a až potom“. Veta hovorí dve veci naraz (pozrite sa na obrázok):
skúsme použiť túto vetu na vyriešenie problému.
Úloha: je daný pravidelný šesťhranný ihlan. Nájdite uhol medzi čiarami a.

Riešenie:
Vzhľadom na to, že v pravidelnej pyramíde vrchol pri premietnutí padá do stredu základne, ukazuje sa, že priamka je projekciou priamky.
Ale vieme, že je v pravidelnom šesťuholníku. Aplikujeme vetu o troch kolmiciach:
A napíšeme odpoveď: .
KOMNOSŤ PRIAMYCH ČIAR V PRIESTORE. STRUČNE O HLAVNÝCH VECIACH
Kolmosť dvoch čiar.
Dve čiary v priestore sú kolmé, ak je medzi nimi uhol.
Kolmosť priamky a roviny.
Čiara je kolmá na rovinu, ak je kolmá na všetky čiary v tejto rovine.
Kolmosť rovín.
Roviny sú kolmé, ak je uhol medzi nimi rovnaký.
Kritérium kolmosti rovín.
Dve roviny sú kolmé vtedy a len vtedy, ak jedna z nich prechádza cez kolmicu na druhú rovinu.
Veta o troch kolmých:

No, téma je ukončená. Ak čítate tieto riadky, znamená to, že ste veľmi cool.
Pretože len 5% ľudí je schopných niečo zvládnuť sami. A ak dočítate až do konca, tak ste v týchto 5%!
Teraz to najdôležitejšie.
Pochopili ste teóriu na túto tému. A opakujem, toto... toto je proste super! Už teraz ste lepší ako drvivá väčšina vašich rovesníkov.
Problém je, že to nemusí stačiť...
Prečo?
Za úspešné absolvovanie Jednotnej štátnej skúšky, za vstup na vysokú školu s obmedzeným rozpočtom a HLAVNE, na celý život.
nebudem ta o nicom presviedcat, poviem len jedno...
Ľudia, ktorí získali dobré vzdelanie, zarábajú oveľa viac ako tí, ktorí ho nezískali. Toto je štatistika.
Ale to nie je to hlavné.
Hlavne, že sú ŠŤASTNEJŠÍ (existujú také štúdie). Možno preto, že sa pred nimi otvára oveľa viac príležitostí a život sa stáva jasnejším? neviem...
Ale zamysli sa nad sebou...
Čo je potrebné na to, aby ste boli na jednotnej štátnej skúške lepší ako ostatní a nakoniec boli... šťastnejší?
ZÍSKAJTE SI RUKU RIEŠENÍM PROBLÉMOV V TEJTO TÉME.
Na skúške od vás nebudú žiadať teóriu.
Budete potrebovať riešiť problémy s časom.
A ak ste ich nevyriešili (VEĽA!), určite niekde urobíte hlúpu chybu alebo jednoducho nebudete mať čas.
Je to ako v športe – treba to veľakrát zopakovať, aby ste vyhrali.
Nájdite kolekciu kdekoľvek chcete, nutne s riešeniami, podrobnou analýzou a rozhodni sa, rozhodni sa, rozhodni sa!
Môžete využiť naše úlohy (voliteľné) a my ich, samozrejme, odporúčame.
Aby ste mohli lepšie využívať naše úlohy, musíte pomôcť predĺžiť životnosť učebnice YouClever, ktorú práve čítate.
Ako? Sú dve možnosti:
- Odomknite všetky skryté úlohy v tomto článku -
- Odomknite prístup ku všetkým skrytým úlohám vo všetkých 99 článkoch učebnice - Kúpte si učebnicu - 899 RUR
Áno, takýchto článkov máme v našej učebnici 99 a prístup ku všetkým úlohám a všetkým skrytým textom v nich je možné okamžite otvoriť.
Prístup ku všetkým skrytým úlohám je poskytovaný po CELÚ životnosť stránky.
Na záver...
Ak sa vám nepáčia naše úlohy, nájdite si iné. Len neostávajte pri teórii.
„Rozumiem“ a „Viem vyriešiť“ sú úplne odlišné zručnosti. Potrebujete oboje.
Nájdite problémy a riešte ich!
